少儿编程让很多问题简单化，其中不泛一笔画问题，该问题引起很多人关注，这个问题是经典的数学问题，那么究竟什么是一笔画问题呢？用通常的方法确实复杂难以让人懂得，但是少儿编程中的方法可以让问题简单化。

什么是“一笔画”问题？

即平面上由曲线段构成的一个图形能不能一笔画成，使得在每条线段上都不重复？例如汉字“日”和“中”字都可一笔画，而“田”和“目”则不能。我们可以构造一个多维空间的无穷个两两相连区域一笔画。

我想大家对“签名”这个词一定都不陌生，拿起笔，刷刷几下，一个突显个性的签名就产生了。但是模仿签名就很困难。因为很多人的签名是一笔画成的，当你模仿时，连接处可能会有空隙，而且这个感觉跟一笔画出来的肯定是不一样。

一笔画问题如何实现？

我们做一个小游戏，请大家看这个图形：

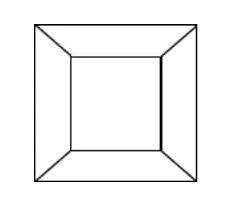
有点像“回”字，你能不能从某一点出发，不重复地一笔把它画出来？这就是中国民间古老的一笔画游戏。

这类“一笔画”问题中最著名的当属“哥尼斯堡七桥问题”了。

什么是七桥问题？

十八世纪的东普鲁士，有一条风景优美的河流，河流汇合处有两座小岛，河上有7座桥，有人关于这7座桥提出了一个问题：一个散步者能否一次走遍7座桥，而且每座桥只通过一次，最后仍回到起始地点。这个问题看起来似乎很简单，然而许多人作过尝试始终没有能找到答案。因此，一群大学生就写信给著名的瑞士数学家欧拉，向他请教如何解决这个七桥问题。

欧拉猜想，也许根本不可能不重复地一次走遍这七座桥，并很快证明了这样的猜想是正确的。

如何用少儿编程解决七桥问题？

聪明的欧拉想到，可以把这四处地点用A,B,C,D四个点来表示，同时将七座桥表示成连结其中两点的七条线，就得到这样一张图。一个人不重复地走遍所有的七座桥，就相当于从图中某一点出发，不重复地一笔画出图来。这样，“七桥问题”就转化为“一笔画”问题了。

欧拉注意到，如果一个图能一笔画成，那么一定有一个起点开始画，也有一个终点。图上其它的点是“过路点”。

这些点有什么特征呢？

“过路点”：“有进有出”的点，有一条边进这点，那么就要有一条边出这点。

“起点”：有出无进。

“终点”：有进无出。

现在对照七桥问题的图，A点连有3条边，B点连有5条边，C点D点各连3条边，所以欧拉得出的结论是这个图肯定不能一笔画成，也就是说要想不重复的走遍这七座桥是不可能的。

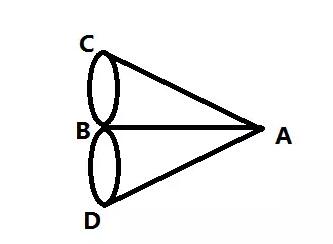
图中的每条边都有两个结点，而且互不相交。如果一个图中的任意两个结点，都可以找到图中的某条弧线，把它们连接起来，那么，这样的图就称为连通的。每个结点所连的边的条数叫做这个结点的度数，度数是偶数就称为偶点，度数是奇数则称为奇点。

欧拉的结论用图论的语言叙述，那就是：

如果一个图是连通的并且奇点的个数等于0或2，那么它可以一笔画出；否则它不可以一笔画出。

用所学结论验证下列图形能否一笔画出

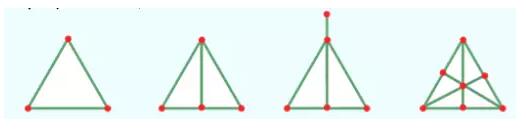
答案

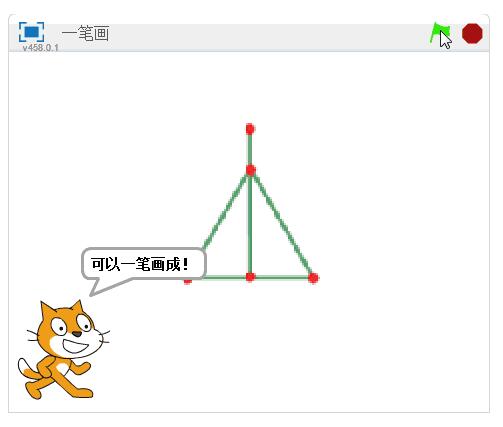
以上是有关一笔画问题的相关解析，通过少儿编程，你是否发现，很多难题变的竟是如此简单，让我们深入了解少儿编程，让更多难点解开吧！

同程同美编程数学让孩子用编程的思维来思考，在快乐的环境中学习数学思维能力，让枯燥乏味的数学更有趣、更立体、更实用，可实验、可观感、可理解，数学提分不用愁。既可以提升学习数学的能力，还能了解编程知识，一举两得。