ArrayList集合有何用途？有何用法？ArrayList也是插入时有序，需要自己重写排序方法进行排序。下面我们去详细了解一下。

有关非线程安全的集合小结

1.ArrayList为什么实现RandomAccess接口

因为指针的原因

2.参数含义

EMPTY_ELEMENTDATA 空实例的默认集合

DEFAULT_CAPACITY 集合的默认长度10

DEFAULTCAPACITY_EMPTY_ELEMENTDATA ：用于缺省大小的空实例的共享空数组实例。我们将此与EnvyTyEeltDATA区分开来，以知道在添加第一个元素时要膨胀多少。

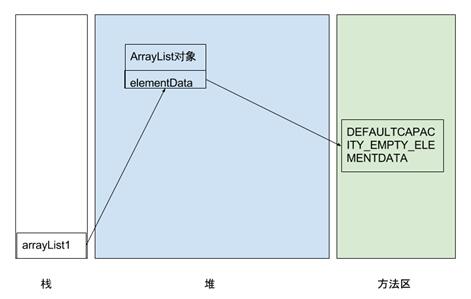
3. 构造方法

我们可以发现，默认的构造函数中就只有一句话。但也表明了自己的真实身份，就是一个控制一个 Object 数组的类。

但是，为什么还要给 elementData 赋值一个静态的Object数组呢？为什么不直接 new 一个Object 数组呢？我们知道，static final 修饰的常量存在于内存中的方法区，且有且仅有一个实例，所以当我们再次创建一个 ArrayList 的对象时，elementData 指向的还是同一个 DEFAULTCAPACITY_EMPTY_ELEMENTDATA。

由图可以看出，DEFAULTCAPACITY_EMPTY_ELEMENTDATA 在这里充当的是一个缓冲区的作用，避免创建多个无用的数组

/*

传递一个集合给ArrayList，它首先会将集合转换成数组赋值给elementData

之后判断数组长度，如果等于0，则将elementData赋值为EMPTY_ELEMENTDATA

如果不等于0，还需要判断接受过来的数组(现在是elementData)是否是Object[]类型的

如果不是的化，将它转换成Object[]类型(根据注释，toArray方法有可能得到的不是Object[]类型)

*/

public ArrayList(Collection<? extends E> c) {

elementData = c.toArray();

if ((size = elementData.length) != 0) {

// c.toArray might (incorrectly) not return Object[] (see 6260652)

if (elementData.getClass() != Object[].class)

elementData = Arrays.copyOf(elementData, size, Object[].class);

} else {

// replace with empty array.

this.elementData = EMPTY_ELEMENTDATA;

}

}

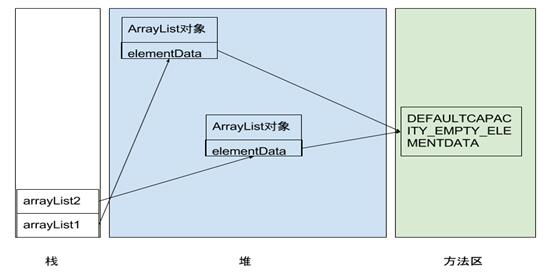
4. clone和赋值的区别

区别在于赋值操作会使两个引用指向同一个对象，无论操作任何一个对象都会是内存中的对象发生变化，而clone的操作是在相同对象的基础上，进行对象的重建。

扩展：时间复杂度问题：

一般情况下，算法的基本操作重复执行的次数是模块n的某一函数f(n),因此，算法的时间复杂度记做T(n) = O(f(n))。随着模块n的增大，算法执行的时间增长率f(n)的增长率成正比，所以f(n)越小，算法的时间复杂度越低，算法的效率越高。

常数时间复杂度：固定运行一次的常数

O(1)的算法是一些运算次数为常数的算法。例如：

temp=a;a=b;b=temp;

上面语句共三条操作，单条操作的频度为1，即使他有成千上万条操作，也只是个较大常数，这一类的时间复杂度为O(1)。

线性时间复杂度：O(n)=2n+1

O(n)的算法是一些线性算法。例如：

sum=0；

for(i=0;i<n;i++)

sum++；

上面代码中第一行频度1，第二行频度为n，第三行频度为n，所以f(n)=n+n+1=2n+1。所以时间复杂度O(n)。这一类算法中操作次数和n正比线性增长。

平方时间复杂度: O(n)=n*n

1.去掉运行时间中的所有加法常数。

2.只保留最高阶项。

3.如果最高阶项存在且不是1，去掉与这个最高阶相乘的常数得到时间复杂度

for(inti = 0; i < n; i++) {

for(intj = i; j < n; j++) {

// do .....

}

}

对数时间复杂度: O(log2n)

O(logn) 一个算法如果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。举个栗子：

int i=1;

while (i<=n)

i=i*2;

上面代码设第三行的频度是f(n), 则：2的f(n)次方<=n;f(n)<=log₂n，取最大值f(n)= log₂n，所以T(n)=O(log₂n ) 。